Ako nájsť oblasť rovnoramenného trojuholníka

Matematika a najmä geometria podľaprieskumy školákov, jedna z najobľúbenejších hodín a to všetko preto, lebo vás naučia veľké množstvo vzorcov, ktoré v živote nenašli praktické aplikácie v 90% súčasných dospelých. Ale na chvíľu sa učíme vzorce, vyriešime problémy, nerobíme rovnice nie pre to, že môžu byť užitočné pre nás v živote, ale preto, že sa rozvíja myslenie a logika. Dokonca aj starí grécki mudrci povedali, že ľudský intelekt sa môže merať znalosťou matematických vied. A keďže ste sa rozhodli zoznámiť sa s aplikáciou vzorcov pre rovnoramenný trojuholník - berieme sa do ruky a čítame celý článok.
Skôr ako začnete odpovedať na otázku, ako nájsťoblasť rovnoramenného trojuholníka a prejdeme do praktickej časti článku, kde sú uvedené vzorce a výpočty, označíme samotný koncept pre seba. Rovnoramenný trojuholník je trojuholník, v ktorom sú dve z troch strán rovnaké v dĺžke, nazývané bočné strany. V prípade pravidelného trojuholníka, kde sú všetky strany rovnaké, je tiež považované za rovnoramenné, ale naopak, ak je izoscelový trojuholník považovaný za správny - je falošný.
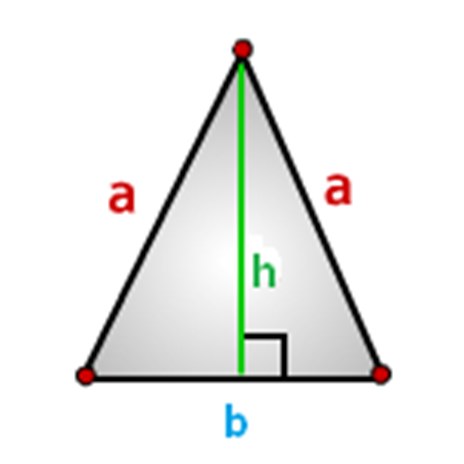
Boky trojuholníka by mali byť označené, budeme to robiť takto, ako je znázornené na obrázku nižšie, kde: a - sides, b-base a h-height.
Ako vypočítať plochu rovnoramenného trojuholníka, vzorce.
Potom, čo sme urobili notáciu o výške, stranách a uhle, môžeme začať riešiť tento problém.
Najprv určite, čo vieme.
Ak je výška a spodná - potom klasický vzorec (* - násobenie):
S = ½ * b * h
Nahraďme napríklad čísla, kde: h = 16, b = 18, dostaneme nasledovné:
S = 1/2 * 18 * 16 = 9 * 16 = 144;
Plocha rovnoramenného trojuholníka je S = 144 cm2
Existujú aj iné vzorce, ktoré nám pomôžuako poznať oblasť rovnoramenného trojuholníka. Jeden takýto vzorec je Heronova metóda. Nechcem napísať zložitý vzorec, berieme na základe toho skrátený:
S = ¼ b √4 * a2-b2
Je zrejmé, že b je základňa a rovnaké stránky. Vzorec je vhodný v prípade, keď h-výška nie je známa.
Nahradením hodnôt nechajte a = 6, b = 3, získame nasledovné:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Môžete použiť výpočet plochy, ktorá sa rovná stranám trojuholníka a uhlu medzi stranami:
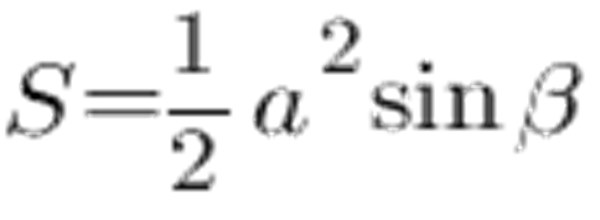
Podľa sínusovej tabuľky sa uhol pri 45 ° rovná 0,7071, strana a a nech je 6 cm, získame nasledovné:
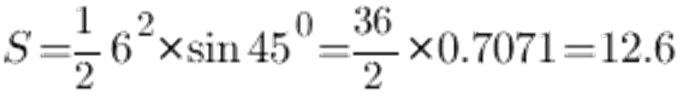
V dôsledku toho je oblasť rovnoramenného trojuholníka 12,6 cm2.
Existujú aj spôsoby výpočtu oblasti vrátaneaj v prípade rovnoramenného trojuholníka, ale sú pomerne komplikované a nevzťahujú sa na "elementárne" výpočty, ako sú uvedené vyššie, v pojmoch komplexnej matematiky. A nestojí za to hovoriť o veciach, ktoré ani učitelia so skúsenosťami nebudú rozumieť.
Takže si môžete vzdychať úľavumalý priebeh geometrie na nájdenie oblasti rovnoramenného trojuholníka bude považovaný za úplný a vedomosti získané v dôsledku čítania článku sa naučia "päť".